Dua Sejoli

Soal#

Informasi#

• Sumber: CompFest 9 - Penyisihan CPC Senior
• Tanggal: 2017-08-12

Arsip#

• TLX

Ringkasan#

Terdapat $N$ tempat pertemuan dan $N$ jalan dua arah. Terdapat setidaknya satu rute di antara dua tempat pertemuan. Berapa minimum jalan yang harus ditutup untuk memisahkan pasangan dengan laki-laki berada di tempat pertemuan ke-$X_j$ dan perempuan berada di tempat pertemuan ke-$Y_j$, serta banyaknya cara untuk melakukan hal tersebut (modulo $10^9 + 7$)?

Solusi#

Petunjuk#

Pembahasan#

Mari kita modelkan hubungan tempat pertemuan dan jalan sebagai suatu graf. Tempat pertemuan dan jalan secara berurutan direpresentasikan sebagai simpul dan sisi pada graf. Graf ini merupakan keluarga dari pseudotree (pseudoforest dengan satu komponen terhubung). Graf pada soal ini memiliki tepat satu siklus, yang bisa disebut sebagai 1-tree atau unicyclic graph. Kita bisa melakukan partisi pada graf menjadi satu siklus dan beberapa pohon sedemikian sehingga tiap pohon memiliki simpul pada siklus. Setiap pohon akan memiliki simpul akar (root) yang terhubung satu sama lain sehingga membentuk satu siklus.

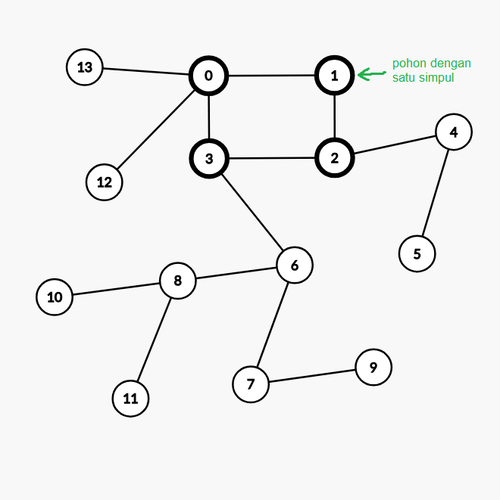
Terdapat beberapa kasus penempatan simpul $X_j$ dan $Y_j$ pada graf.

• Simpul $X_j$ dan $Y_j$ berada pada pohon yang sama.
  Pada kasus ini, kita dapat menutup 1 jalan pada lintasan (path) di antara simpul $X_j$ dan simpul $Y_j$ untuk menghasilkan penutupan jalan paling minimum. Banyaknya cara untuk menutup jalan adalah panjang (banyaknya jalan) dari lintasan tersebut.
• Simpul $X_j$ dan $Y_j$ berada pada pohon yang berbeda, namun kedua berada pada simpul akar.
  Terdapat dua lintasan berbeda di antara kedua simpul. Kita harus menutup satu jalan pada masing-masing lintasan tersebut. Oleh karena itu, kita dapat menutup 2 jalan untuk menghasilkan penutupan jalan paling minimum. Banyaknya cara untuk menutup jalan adalah panjang lintasan pertama dikali dengan panjang lintasan kedua.
• Simpul $X_j$ dan $Y_j$ berada pada pohon yang berbeda dan salah satu atau keduanya tidak berada pada simpul akar.
  Pada kasus ini, kita dapat menutup 1 jalan untuk menghasilkan penutupan jalan paling minimum. Jalan yang ditutup adalah jalan yang tidak termasuk ke dalam siklus. Banyaknya cara untuk menutup jalan adalah kedalaman (depth, panjang lintasan dari suatu simpul pada pohon ke simpul akar) dari $X_j$ ditambah kedalaman dari $Y_j$.

Mula-mula, kita akan mencari siklus dan menyimpannya ke dalam sebuah array. Simpul yang saling bertetangga pada siklus juga akan bersebelahan pada array. Elemen pertama dan terakhir pada array juga dianggap bersebelahan.

Misal $\text{index}(v)$ menyatakan indeks simpul $v$ pada array. Panjang salah satu lintasan di antara simpul $X_j$ dan $Y_j$ pada siklus adalah $|\text{index}(X_j) - \text{index}(Y_j)|$. Sedangkan panjang lintasan lainnya adalah $\text{panjang siklus} - |\text{index}(X_j) - \text{index}(Y_j)|$.

Kita juga perlu sebuah prosedur yang efisien untuk menemukan panjang lintasan di antara dua simpul pada suatu pohon. Kita akan menggunakan informasi kedalaman dan fungsi yang menghasilkan LCA (lowest common ancestor) dari dua simpul. LCA dari dua buah simpul $u$ dan $v$ didefinisikan sebagai sebuah simpul $w$ di mana

• kita bisa mencapai $u$ dan $v$ dengan menelusuri nol atau lebih jalan di bawah simpul $w$ dan
• kedalaman dari simpul $w$ adalah yang terbesar dari semua simpul yang memenuhi kondisi sebelumnya.

Misal $\text{depth}(v)$ menyatakan kedalaman simpul $v$ dan $\text{lca}(u, v)$ adalah LCA dari simpul $u$ dan $v$. Panjang lintasan di antara simpul $X_j$ dan $Y_j$ adalah $\text{depth}(X_j) + \text{depth}(Y_j) - 2 \cdot \text{depth}(\text{lca}(X_j, Y_j))$.

Fungsi $\text{index}$, $\text{depth}$, dan $\text{lca}$ dapat diprekomputasi terlebih dahulu ke dalam array. Untuk melakukan prekomputasi fungsi $\text{depth}$ pada suatu pohon, kita bisa menjelajahi graf dimulai dari simpul akar pada pohon tersebut. Untuk melakukan prekomputasi fungsi $\text{lca}$, kita bisa menggunakan struktur data dengan kombinasi algoritma seperti Euler's tour + struktur data yang mendukung range minimum query secara efisien atau sparse table + binary lifting. Solusi saya menggunakan sparse table dan binary lifting untuk menghitung fungsi $lca$ secara efisien.

Kode#

#include <iostream>
#include <vector>
using namespace std;
typedef pair <int, int> pii;

const int MAXN = 50000;
const int MOD = 1E9 + 7;

int T, N, Q, LOG_N;
int cycle_start, cycle_size;
int parent[MAXN];
int cycle_idx[MAXN];
int depth[MAXN];
int sparta[MAXN][20];
vector <pii> al[MAXN];
vector <int> cycle;
bool vis[MAXN];
bool push_cycle;

void get_cycle(const int& u, const int& idx = -1){
    vis[u] = 1;
    for(const pii& p : al[u]){
        if(cycle_start != -1) break;
        if(p.second == idx) continue;
        if(p.second != idx && vis[p.first]){
            cycle_start = p.first;
            push_cycle = 1;
            break;
        }
        get_cycle(p.first, p.second);
    }

    if(push_cycle){
        cycle.push_back(u);
        if(u == cycle_start) push_cycle = 0;
    }
}

void get_parent(const int& u, const int& prev = -1){
    parent[u] = prev;
    for(const pii& p : al[u]){
        if(p.first == prev || cycle_idx[p.first] != -1)
            continue;
        depth[p.first] = depth[u] + 1;
        get_parent(p.first, u);
    }
}

void construct_sparta(){
    for(int i = 0; i < N; i++)
        sparta[i][0] = parent[i];

    for(int j = 1; j <= LOG_N; j++)
        for(int i = 0; i < N; i++){
            int v = sparta[i][j - 1];
            if(v == -1) sparta[i][j] = -1;
            else sparta[i][j] = sparta[v][j - 1];
        }
}

int get_root(int v){
    int jump = depth[v];
    for(int i = LOG_N; 0 <= i; i--)
        if((1 << i) <= jump){
            jump -= 1 << i;
            v = sparta[v][i];
        }
    return v;
}

int lca(int u, int v){
    if(depth[v] < depth[u])
        swap(u, v);

    int diff = depth[v] - depth[u];
    for(int i = LOG_N; 0 <= i; i--)
        if((1 << i) <= diff){
            diff -= 1 << i;
            v = sparta[v][i];
        }

    if(u == v) return v;

    for(int i = LOG_N; 0 <= i; i--)
        if(sparta[u][i] != sparta[v][i]){
            u = sparta[u][i];
            v = sparta[v][i];
        }
    return sparta[v][0];
}

int main(){
    cin.tie(0)->sync_with_stdio(0);
    cin >> T;

    while(T--){
        cin >> N;
        cycle.clear();
        for(int i = 0; i < N; i++){
            al[i].clear();
            vis[i] = 0;
            parent[i] = -1;
            cycle_idx[i] = -1;
            depth[i] = 0;
        }

        int u, v;
        for(int i = 0; i < N; i++){
            cin >> u >> v;
            u--, v--;
            al[u].push_back({v, i});
            al[v].push_back({u, i});
        }

        cycle_start = -1;
        push_cycle = 0;
        get_cycle(0);

        for(size_t i = 0; i < cycle.size(); i++)
            cycle_idx[cycle[i]] = i;

        for(int i = 0; i < N; i++)
            if(cycle_idx[i] != -1)
                get_parent(i);

        int k = 1;
        LOG_N = 0;
        while(k < N){
            k <<= 1;
            LOG_N++;
        }
        construct_sparta();

        cycle_size = cycle.size();
        cin >> Q;
        while(Q--){
            cin >> u >> v;
            u--, v--;
            if(get_root(u) == get_root(v))
                cout << "1 " << (depth[u] + depth[v] - 2 * depth[lca(u, v)]) % MOD << '\n';
            else if(cycle_idx[u] != -1 && cycle_idx[v] != -1){
                int dist = max(cycle_idx[u], cycle_idx[v]) - min(cycle_idx[u], cycle_idx[v]);
                cout << "2 " << (1LL * dist * (cycle_size - dist)) % MOD << '\n';
            }
            else
                cout << "1 " << (depth[u] + depth[v]) % MOD << '\n';
        }
    }
    return 0;
}