Xor-Or

Soal#

Informasi#

• Sumber: CompFest 9 - Final CPC Senior
• Tanggal: 2017-09-17

Arsip#

• TLX

Ringkasan#

Diberikan sebuah graf tak berarah yang dapat memiliki self-loop namun tidak dipastikan terhubung. Setiap sisi (edge) memiliki bobot (weight) yang disebut dengan nilai keseraman. Didefinisikan

• Rute sebagai lintasan (path) yang membolehkan simpul (vertex) dan sisi untuk dilewati lebih dari sekali.
• Nilai keseraman rute sebagai bitwise XOR dari semua nilai keseraman sisi yang dilewati rute tersebut.
• $S(i, j)$ sebagai himpunan yang berisi semua nilai keseraman rute yang mungkin dari simpul $i$ ke simpul $j$.
• $F(i, j)$ sebagai bitwise OR dari semua anggota $S(i, j)$ dan bernilai 0 apabila $S(i, j)$ kosong.

Tentukan jumlahan dari $F(i, j)$ untuk setiap simpul $i$ dan $j$ di mana $i < j$.

Solusi#

Petunjuk#

Pembahasan#

Sedikit trivia, rute yang didefinisikan pada soal ekuivalen dengan definisi walk, lebih tepatnya open walk.

Seperti soal bitmasking pada umumnya, mari kita cari tahu apakah persoalan ini dapat kita selesaikan dengan memecahkan persoalan lebih kecil untuk setiap posisi bit.

Misalkan kita saat ini bekerja pada bit ke-$p$. Ingat bahwa $S(i, j)$ adalah himpunan semua nilai keseraman rute yang mungkin dari $i$ ke $j$. Apabila bit ke-$p$ dari salah satu anggota himpunan ini bernilai 1, dengan sifat operasi bitwise OR, maka bit ke-$p$ pada $F(i, j)$ juga bernilai 1.

Untuk posisi bit ke-$p$, sebuah rute dikatakan memenuhi apabila bit ke-$p$ pada nilai keseraman rute tersebut bernilai 1. Jadi untuk setiap posisi bit, kita perlu mencari semua rute yang memenuhi dari setiap pasang simpul $i$ dan $j$.

Gambaran kasar algoritma yang akan kita buat adalah sebagai berikut.

answer = 0
for each bit position p:
    route_cnt = 0
    for all i, j where i < j:
        if there is a valid route:
            route_cnt++
    answer += route_cnt * 2^p

Bagian terpenting dari algoritma di atas adalah bagaimana cara menemukan salah satu rute yang memenuhi. Untuk memudahkan ilustrasi, mari kita buat sebuah graf.

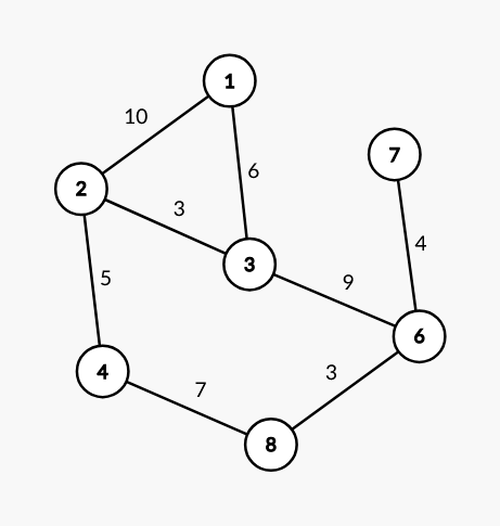
Misalkan algoritma kita saat ini bekerja pada bit ke-1 (bit ke-2 dari kanan). Kita akan membuat graf salinan dengan bobot setiap sisi diganti dengan bit ke-1 pada bobot asli sisi tersebut.

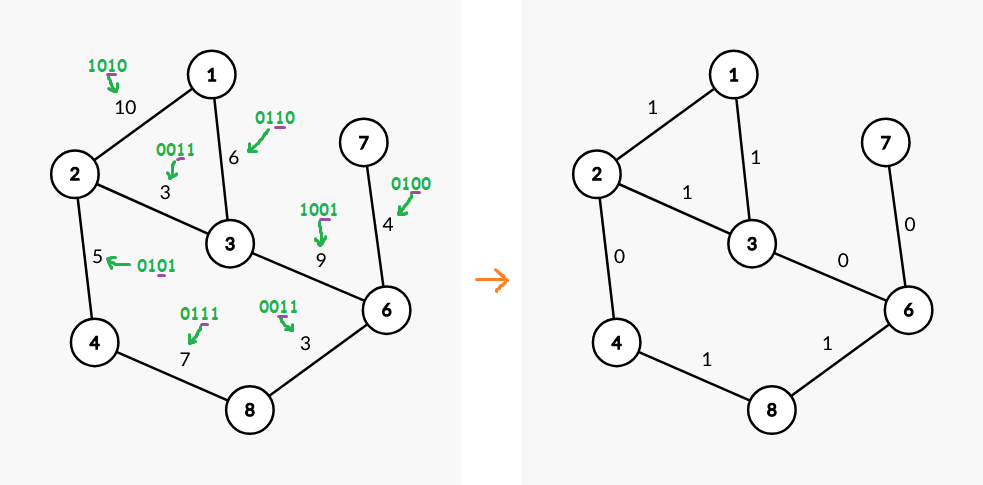
Pada graf salinan, setiap rute akan memiliki dua kemungkinan nilai keseraman: 0 atau 1. Rute yang valid memiliki nilai keseraman 1. Kita lihat beberapa contoh pasangan $i$ dan $j$ dan salah satu rute yang memenuhi.

• Untuk $i$ = 1 dan $j$ = 6, kita bisa memilih rute 1 - 3 - 6.
• Untuk $i$ = 1 dan $j$ = 8, kita bisa memilih rute 1 - 2 - 3 - 6.
• Untuk $i$ = 6 dan $j$ = 7, kita bisa memilih rute 6 - 8 - 4 - 2 - 3 - 6 - 7. Ingat bahwa kita bisa melewati simpul maupun sisi lebih dari sekali. Jadi, rute 6 - 3 - 2 - 1 - 3 - 6 - 7 juga termasuk rute yang memenuhi.

Jika kita lakukan hal yang sama untuk setiap pasang simpul yang lain, dapat kita lihat bahwa setiap pasang simpul pasti memiliki rute yang valid. Sepertinya terdapat properti dari graf yang memungkinkan kita untuk menemukan rute yang valid untuk seluruh pasang simpul.

Mari kita telurusi graf salinan dimulai dari suatu simpul awal dan mencatat nilai keseraman rute dari simpul awal ke semua simpul yang dikunjungi. Kita gunakan algoritma depth-first search untuk menelusurinya. Kita catat nilai keseraman rute dengan array bernama value. Berikut adalah pseudocode dari algoritma penelusuran tersebut.

dfs(u):
    mark u as visited
    for each v neighbor of u:
        w is weight of edge (u, v)
        if v is not visited:
            value[v] = value[u] xor w
            dfs(v)
        else
            do something

Bagian yang menarik dari algoritma di atas terdapat pada kasus di mana simpul tetangga (v) yang akan kita telusuri ternyata sudah dikunjungi. Kasus ini menandakan bahwa kita telah menemukan sebuah siklus. Terlebih lagi, apabila value[v] tidak sama dengan value[u] xor w (u adalah simpul saat ini), maka kita telah menemukan cara untuk membalikkan nilai keseraman rute ke simpul v dengan melewati siklus ini. Dengan kata lain, rute yang dimulai dari suatu simpul pada siklus ini, melewati semua simpul pada siklus tanpa mengunjungi sisi yang sama, dan kembali lagi ke simpul semula akan memiliki nilai keseraman 1. Kita sebut siklus ini sebagai siklus ganjil.

Kita akan buktikan secara informal bahwa terdapat cara untuk mencari rute memenuhi untuk setiap pasang simpul apabila terdapat siklus ganjil. Definisikan rute sederhana sebagai rute yang tidak melewati sisi dan simpul lebih dari sekali. Bagi menjadi dua skenario:

• Kita langsung menemukan rute sederhana yang memenuhi dari simpul $i$ ke simpul $j$ tanpa melewati siklus ganjil, atau
• kita tidak menemukan rute sederhana seperti skenario sebelumnya. Oleh karena itu, kita bisa memanfaatkan siklus ganjil untuk membuat rute yang memenuhi. Rute yang memenuhi dari simpul $i$ ke simpul $j$ tersusun atas

1. rute sederhana dari $i$ ke $j$,
2. sebuah rute dari $j$ ke sembarang simpul pada siklus ganjil (kita sebut simpul ini sebagai $k$),
3. melewati siklus ganjil dari $k$ dan berakhir di $k$, dan
4. berbalik arah melewati rute kedua (dari $k$ ke $j$).

Nilai keseraman rute tersebut adalah 0 xor z xor 1 xor z = 1, dengan z adalah nilai keseraman rute dari $j$ ke $k$ dan sebaliknya.

Bisa kita simpulkan bahwa apabila terdapat siklus ganjil pada graf dengan simpul sebanyak $N$, maka banyaknya rute yang memenuhi adalah $\frac{N(N - 1)}{2}$.

Lalu, bagaimana jika tidak ada siklus ganjil sama sekali? Untuk ilustrasi, kita bisa hilangkan sisi $(2, 3)$ pada graf salinan di atas untuk mendapatkan graf yang tidak mengandung siklus ganjil.

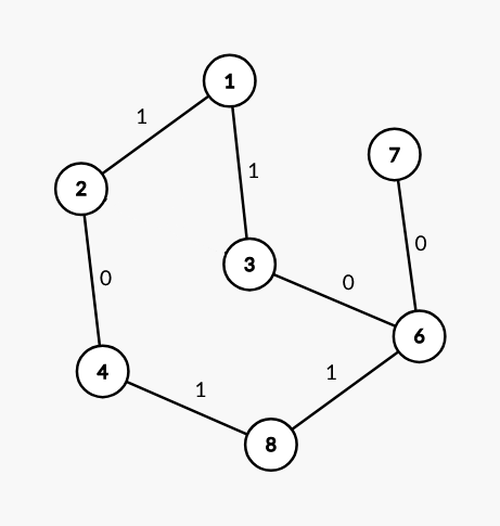
Kemudian, kita jalankan algoritma penelusuran sebelumnya dimulai dari sembarang simpul, misalnya simpul 1. Tulisan berwarna merah menandakan value dari simpul di dekatnya.

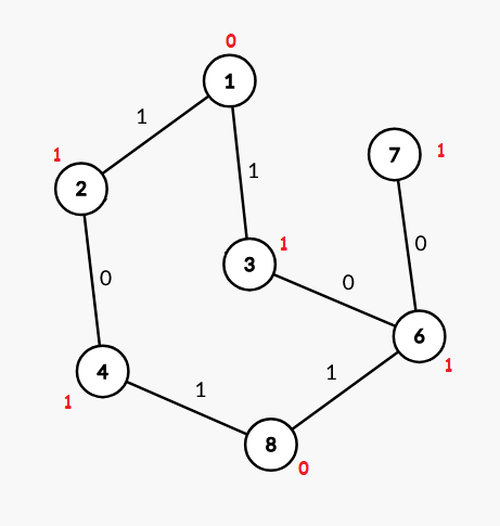
Mari kita kelompokkan semua simpul berdasarkan value. Semua simpul dengan value 0 berada di kelompok $L$ dan semua simpul dengan value 1 berada di kelompok $R$. Terlihat bahwa untuk mencapai suatu simpul di kelompok $R$ dari simpul di kelompok $L$, kita perlu melewati satu sisi dengan nilai keseraman 1. Begitu pula jika kita mencapai simpul di $L$ dari $R$. Dari observasi ini, bisa kita simpulkan bahwa semua rute dari simpul di $L$ menuju simpul di $R$ atau sebaliknya, pasti merupakan rute yang memenuhi.

Misal banyaknya simpul pada kelompok $L$ dan $R$ berturut-turut adalah $|L|$ dan $|R|$. Maka, banyaknya rute yang memenuhi pada graf yang tidak memiliki siklus ganjil adalah $\frac{|L| \cdot |R| + |R| \cdot |L|}{2} = |L| \cdot |R|$. Kita harus membagi dua untuk menghindari double counting, yakni menghitung sisi $(i, j)$ dengan $i > j$ yang tidak sesuai dengan syarat pada soal.

Jangan lupakan bahwa graf bisa saja tidak terhubung. Hal ini dengan mudah ditangani dengan melakukan penelusuran untuk setiap simpul yang belum dikunjungi.

Kode#

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
typedef long long int lli;
typedef pair <int, int> pii;

const int MAXN = 30000;

int T, N, M;
lli vcnt, cnt[2];
char value[MAXN];
vector <pii> al[MAXN];
queue <int> q;

lli dfs(int u, const int& pos){
    vcnt = cnt[0] = cnt[1] = 0;

    value[u] = '0';
    q.push(u);

    bool odd_cyc = 0;
    while(!q.empty()){
        u = q.front();
        q.pop();
        vcnt++;
        cnt[value[u] & 1]++;

        for(const pii& p : al[u]){
            const int& v = p.first;
            const int w = ((p.second >> pos) & 1);
            if(value[v] == '.'){
                value[v] = value[u] ^ w;
                q.push(v);
            }
            else if(value[v] != (value[u] ^ w))
                odd_cyc = 1;
        }
    }

    if(odd_cyc) return vcnt * (vcnt - 1)/2;
    else return cnt[0] * cnt[1];
}

int main(){
    ios_base::sync_with_stdio(0);

    cin >> T;
    while(T--){
        cin >> N >> M;

        for(int i = 0; i < N; i++)
            al[i].clear();

        int Ui, Vi, Wi, len;
        int mx_pos = 0;
        for(int i = 0; i < M; i++){
            cin >> Ui >> Vi >> Wi;
            Ui--, Vi--;

            al[Ui].push_back({Vi, Wi});
            al[Vi].push_back({Ui, Wi});

            len = 0;
            while(Wi){
                Wi >>= 1;
                len++;
            }
            mx_pos = max(mx_pos, len);
        }

        int ans = 0;
        for(int pos = 0; pos <= mx_pos; pos++){
            for(int i = 0; i < N; i++)
                value[i] = '.';

            int rcnt = 0;
            for(int src = 0; src < N; src++){
                if(value[src] == '.')
                    rcnt += dfs(src, pos);
            }

            ans += rcnt * (1 << pos);
        }

        cout << ans << '\n';
    }
    return 0;
}